-
#2 Distance Metric 본문
* 3주차 강의 내용입니다.
0) Distance가 무엇인가?
데이터 과학, 데이터를 가공하는데 왜 Distance라는 개념이 튀어나온 것일까? 이유를 알아보기 위해 우선 우리가 일상적으로 사용하고 있는 거리(distance)의 개념에 대해 생각해보자
일상속에서의 Distance?

보통 일상속에서 '거리' 라는 개념은 어디론가 이동해야할 때 등장한다. 시작점이 있고 도착점이 있을 때 이 사이를 이동하기 위해서는 어느정도 걸어야하는지(혹은 탈 것) 나타내는 지표이며 이는 그 사이의 장애물이나 경사 등 요소에 따라 직선이 아닐수도 있다. 반면 시작점과 도착점을 직선으로 잇는 '직선 거리'라는 개념도 존재한다. 위의 예시에서는 파란색 길이 매우 굴곡져있는데, 건물들이 빼곡한 도시에서의 상황을 생각해보자.

길이 굴곡져있다면 시작점과 도착점 사이의 거리(직선 거리 x)를 측정하는 것이 매우 어려울 것이다. 반면 위와 같은 건물이 빼곡히 있는 도시의 경우 건물과 건물 사이를 이동할 때 거의 직각으로 움직이기 때문에 조금은 길이를 가늠하기 쉬워진다. 이러한 상황에서 사용할 수 있는 Distance Metric이 따로 존재하는데 바로 Manhattan Distance이다. 이름이 Manhattan인 이유는 위의 예시 그림이 맨해튼의 지도이며 이와 같이 도시에서 길을 가는 경우 블록을 피해가야 하는데 그런 상황에 적합한 Distance Metric이기 때문이다. 이에 대한 내용은 뒤에서 설명하도록 하고 이제 수학에서의 Distance를 살펴보자
--
1) 다양한 Distance Metric
Pythagorean theorem

사실 우리는 수학에서 두 점 사이의 거리를 구하는 방법에 대해 아주 잘 알고있다. 이름하여 '피타고라스 정리'는 중학교때부터 주구장창 나오는 개념이며 이를 이용하면 직각 삼각형의 원리에 의해 두 점 사이의 거리를 손쉽게 알아낼 수 있다는 것이다. 우리는 이렇게 점과 점 사이(데이터 사이)의 거리를 구하여 두 데이터 간의 유사도에 대해 알아볼 예정이다. 이전 글에서(Linear Algebra) 데이터를 여러개의 components를 지닌 vector로 나타낼 수 있다고 했는데, 만약 components가 두개 뿐인 두 데이터가 있다면 피타고라스 정리만 이용해도 쉽게 두 데이터간의 유사도를 알아낼 수 있다. 하지만 이는 오직 이차원 평면에 존재하는 직각 삼각형의 변을 구하기 위한 정리였으며 데이터의 components가 3개 이상일 경우 피타고라스 정리로 유사도를 측정하기에는 부적합하다.
--
Euclidean Distance

유클리디언 거리는 피타고라스 정리를 다차원으로 확장한 개념이라고 이해하면 될 것 같다. 물론 위의 예시에는 피타고라스 정리와 다를 바 없지만 이를 조금 더 일반화 한다면 3차원 이상의 데이터들도 무리 없이 Distance를 구할 수 있다.

차원의 확장이라고 해서 대단한 것은 없고 그냥 두 component 사이에 차를 구하고 이를 제곱한 값을 더한데에 제곱근을 해준 것이다. 이렇게 하면 i가 2던, 100이던간에 차원 상관 없이 손쉽게 Distance를 구할 수 있다.
--
Manhattan Distance


맨해튼 거리(Manhattan Distance)는 처음 예시에 등장했던 거리 계산법이다. 다시 설명하자면 맨해튼과 같은 도시의 경우 건물들이 빼곡히 있기 때문에 초록색처럼 직선으로 갈 수 없고, 빨강, 노랑, 파랑 처럼 꾸불꾸불 돌아서 가야한다. 이 때 거리를 구하고 싶다면 단순히 시작점의 x축과 도착점의 x축 거리를 더하고, 시작점의 y축과 도착점의 y축 사이의 거리를 더하면 된다. 이는 빨간색 선을 보면 알 수 있다.
--
Cosine Distance
Cosine Distance는 두 벡터간 '각'을 이용해 유사도를 측정하는 방식이다.


두 벡터가 서로 일치할수록 1에 가까워지고 다를수록 -1에 가까워지는 원리를 이용한다.
--
2) Distance 통합하기
Minkowski Distance

Minkowski Distance는 normed vector space에서 Eculidean Distance와 Manhatten Distance를 일반화할 수 있는 Distance Metric이다.
3) Correlation

분산 된 데이터에 대해서 Correlation을 도식화 한 그림이다. 각 데이터들이 배치된 방향과 응집도에 따라 유사도를 나타내며 -1부터 1로 표시한다. 다수의 Components(x1, x2, x3, ...)로 이루어진 데이터가 있다고 하자. 하나의 Component가 달라질 때 또 다른 Component도 달라진다면, 서로 관련이 있는 것이다. 즉, x1이 달라질 때 '직선' 방향으로 x2도 달라진다면, x1과 x2는 선형으로 상관 관계가 있는 것.
4) Mahalanobis Distance
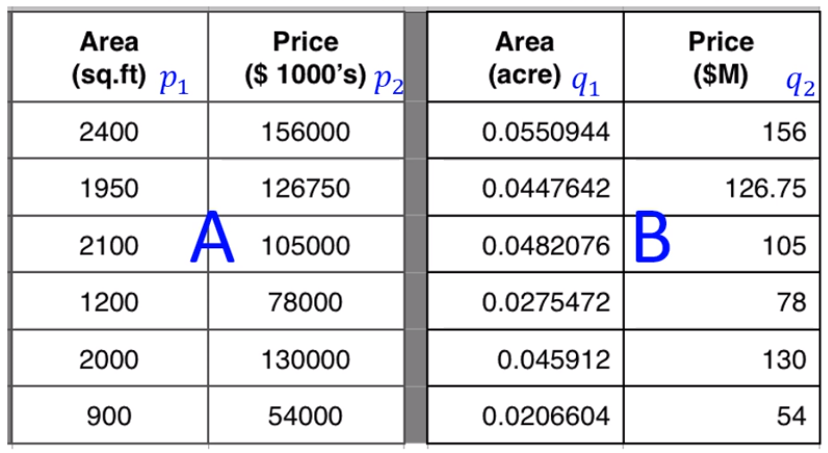
Mahalanobis Distance는 데이터의 Scale에는 상관 없이 두 벡터간의 Correlation을 구할 수 있는 Distance Measure이다. 위 예시 데이터를 보면 좌측과 우측은 동일한 데이터이지만 단위만 다르다. 이 때 단위 즉, scale의 차이 때문에 모델링을 했을 때 서로 다른 데이터라고 결론이 나올 수 있다. Mahalanobis Distance는 이러한 문제를 해결해준다. 1) 각 Component들 사이의 상관 관계를 없애고 2) Scale에 민감하지 않게 정규화 해준다음 3) Euclidean처럼 거리를 계산하면 된다.

'ETC > Data Science' 카테고리의 다른 글
| #5 DNN(Deep Neural Network) (0) | 2020.06.09 |
|---|---|
| #4 Principal Components Analysis (0) | 2020.06.09 |
| #3 Clustering (0) | 2020.06.09 |
| #1 Probability, Statics, Linear Algebra (0) | 2020.06.09 |
| #0 알고리즘 응용 개요 (0) | 2020.06.08 |




